해설지 보는 전략을 정답률 높은지 낮은지에 따라 해설지 보는 전략을 다르게 해야 하는
맞습니다. 정답률에 따른 해설 활용 전략은 수학뿐 아니라 국어, 영어, 탐구 과목 모두에 적용됩니다. 다만 과목 특성에 따라 접근 방식이 약간 달라요.
국어나 영어는 ‘정답률이 낮은 문항’을 볼 때, 단순히 ‘틀리기 쉬운 함정’을 찾는 게 아니라 출제자가 의도한 사고의 흐름을 파악하는 게 핵심이에요. 예를 들어 국어 독서에서 정답률 30% 이하 문제는 대부분 논리 구조나 조건 해석의 미세한 차이에서 갈리죠. 해설지를 볼 때는 ‘왜 오답이 아니라 정답이어야 했는지’를 문장 단위로 짚어야 합니다. 반대로 정답률이 높은 문항은 ‘핵심 문장 찾기 습관’이나 ‘기본 독해 패턴’을 점검하는 용도로 가볍게 확인하면 충분해요.
영어는 정답률이 낮은 문제일수록 어휘보다 문장 구조·접속어 논리에서 오류가 납니다. 그래서 해설을 읽을 때 ‘이 문장이 왜 그렇게 해석돼야 하는지’를 분석해야 하고, 높은 정답률 문제는 오히려 속도 조절 연습용으로 활용하면 됩니다.
탐구 과목은 정답률 분석이 특히 중요합니다. 정답률이 낮은 문제는 개념의 변형, 자료 해석력, 조건 적용 순서를 묻는 경우가 많기 때문이에요. 이런 문제는 해설지를 통해 사고 순서를 복기해야 하고, 반대로 정답률이 높은 문제는 단순 암기나 공식 적용이므로 해설은 짧게 점검만 해도 충분합니다.
요약하자면, 정답률이 낮을수록 ‘사고 과정’을 복기하고, 높을수록 ‘기본기 유지’를 확인하는 게 원칙이에요. 수학뿐 아니라 모든 과목에서 똑같이 적용되는 ‘공부의 효율 공식’이라고 보시면 됩니다.
-
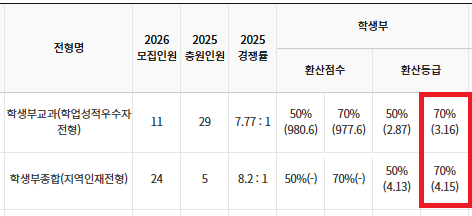
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -
목포에서 롯데월드 가는 법 목포 버스 터미널에서 롯데월드로 갈 수 있는 경로 알려주세요
2025.12.01 -
애니?리뷰 유튜버 찾아주세요ㅠㅠ 무슨 검정머리 남자 캐릭터에 더빙하신분도 남자였던거같은데기승전결로 나눠서 기. 하고 설명하고
2025.12.01 -

발로란트 제한뜨는데 어떻게 해야하나요? 친구가 발로란트 한번해보자고 계정 빌려줬는데 제한이라고 접속이 안되는데 어떻게 해야하나요?
2025.12.01 -

KTX 12월31일 예매 수원이나 서울에서 부산으로 가는 열차를 예매하려고 하는데 언제 열리나요 오늘
2025.12.01 -

한국 지금 쉬었음청년40만명이라는데 4년대학졸업생이 많다던데요 쉬었음청년이 40만명인데 문제가 무엇인가요?
2025.12.01